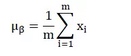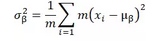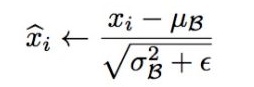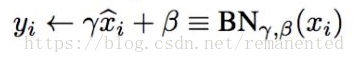Batch Normalization and Group Normalization

#Batch Normalization
Batch Normalization 在深度學習上算是不可或缺的一部分，基本上所有的框架中都會用到它，我記得比較清楚的是，在YOLOV2中作者採用了Batch Normalization 從而提高了4個百分點的Map吧。

##為何要提出Batch Normalization？
在每次給network輸入數據時，都需要進行預處理，比如歸一化之類的，為什麼需要歸一化呢？神經網絡學習過程本質就是為了學習數據分佈，一旦訓練數據與測試數據的分佈不同，那麼網絡的泛化能力也大大降低；另外一方面，一旦每批訓練數據的分佈各不相同(batch 梯度下降)，那麼網絡就要在每次迭代都去學習適應不同的分佈，這樣將會大大降低網絡的訓練速度，這也正是為什麼我們需要對數據都要做一個歸一化預處理的原因。

而且在訓練的過程中，經過一層層的網絡運算，中間層的學習到的數據分佈也是發生著挺大的變化，這就要求我們必須使用一個很小的學習率和對參數很好的初始化，但是這麼做會讓訓練過程變得慢而且複雜m在論文中，這種現象被稱為Internal Covariate Shift。為瞭解決這個問題，作者提出了Batch Normalization。

##Batch Normalization原理
為了降低Internal Covariate Shift帶來的影響，其實只要進行歸一化就可以的。比如，我們把network每一層的輸出都整為方差為1，均值為0的正態分佈，這樣看起來是可以解決問題，但是想想，network好不容易學習到的數據特徵，被你這樣一弄又回到瞭解放前了，相當於沒有學習了。所以這樣是不行的，大神想到了一個大招：變換重構，引入了兩個可以學習的參數γ、β，當然，這也是算法的靈魂所在：

具體的算法流程如下：

Batch Normalization 是對一個batch來進行normalization的，例如我們的輸入的一個batch為：β=x_(1…m)，輸出為：y_i=BN(x)。具體的完整流程如下：

1.求出該batch數據x的均值

2.求出該batch數據的方差

3.對輸入數據x做歸一化處理，得到：

4.最後加入可訓練的兩個參數：縮放變量γ和平移變量β，計算歸一化後的值：

加入了這兩個參數之後，網絡就可以更加容易的學習到更多的東西了。先想想極端的情況，當縮放變量γ和平移變量β分別等於batch數據的方差和均值時，最後得到的yi就和原來的xi一模一樣了，相當於batch normalization沒有起作用了。這樣就保證了每一次數據經過歸一化後還保留的有學習來的特徵，同時又能完成歸一化這個操作，加速訓練。

引入參數的更新過程，也就是微積分的Chain Rule：

Example

def Batchnorm_simple_for_train(x, gamma,beta, bn_param):"""  
param:x   : 輸入數據，設shape(B,L)  
param:gama : 縮放因子  γ  
param:beta : 平移因子  β  
param:bn_param   : batchnorm所需要的一些參數  
   eps      : 接近0的數，防止分母出現0  
   momentum : 動量參數，一般為0.9，0.99， 0.999  
   running_mean ：滑動平均的方式計算新的均值，訓練時計算，為測試數據做準備  
   running_var  : 滑動平均的方式計算新的方差，訓練時計算，為測試數據做準備  
"""  
   running_mean = bn_param['running_mean'] #shape = [B]  
   running_var = bn_param['running_var']   #shape = [B]  
   results = 0. # 建立一個新的變量  
   x_mean=x.mean(axis=0)  # 計算x的均值  
   x_var=x.var(axis=0)    # 計算方差  
   x_normalized=(x-x_mean)/np.sqrt(x_var+eps)       # 歸一化  
   results = gamma * x_normalized + beta            # 縮放平移  
   running_mean = momentum * running_mean + (1 - momentum) * x_mean  
   running_var = momentum * running_var + (1 - momentum) * x_var    #記錄新的值  
   bn_param['running_mean'] = running_mean  
   bn_param['running_var'] = running_var     
   return results , bn_param

這份code首先計算均值和方差，然後歸一化，然後縮放和平移就結束了！但是這是在訓練中完成的任務，每次訓練給一個批量，然後計算批量的均值方差，但是在測試的時候可不是這樣，測試的時候每次只輸入一張圖片，這怎麼計算批量的均值和方差，於是，就有了代碼中下面兩行，在訓練的時候實現計算好mean var測試的時候直接拿來用就可以了，不用計算均值和方差。

running_mean = momentum * running_mean + (1- momentum) * x_mean  
running_var = momentum * running_var + (1 -momentum) * x_var

所以，測試的時候是這樣的：

def Batchnorm_simple_for_test(x, gamma,beta, bn_param):"""  
param:x   : 輸入數據，設shape(B,L)  
param:gama : 縮放因子  γ  
param:beta : 平移因子  β  
param:bn_param   : batchnorm所需要的一些參數  
   eps      : 接近0的數，防止分母出現0  
   momentum : 動量參數，一般為0.9，0.99， 0.999  
   running_mean ：滑動平均的方式計算新的均值，訓練時計算，為測試數據做準備  
   running_var  : 滑動平均的方式計算新的方差，訓練時計算，為測試數據做準備  
"""  
   running_mean = bn_param['running_mean'] #shape = [B]  
   running_var = bn_param['running_var']   #shape = [B]  
   results = 0. # 建立一個新的變量  
   x_normalized=(x-running_mean )/np.sqrt(running_var +eps)       # 歸一化  
   results = gamma * x_normalized + beta            # 縮放平移  
   return results , bn_param

整個過程還是很順的，很好理解的。這部分的內容摘抄自微信公眾號：機器學習算法工程師。一個很好的公眾號，推薦一波。

Batch Normalization 的TensorFlow 源碼解讀，來自知乎：

def batch_norm_layer(x, train_phase,scope_bn):  
   with tf.variable_scope(scope_bn):  
        # 新建兩個變量，平移、縮放因子  
       beta = tf.Variable(tf.constant(0.0, shape=[x.shape[-1]]), name='beta',trainable=True)  
       gamma = tf.Variable(tf.constant(1.0, shape=[x.shape[-1]]), name='gamma',trainable=True)  
       # 計算此次批量的均值和方差  
       axises = np.arange(len(x.shape) - 1)  
       batch_mean, batch_var = tf.nn.moments(x, axises, name='moments')  
       # 滑動平均做衰減  
       ema = tf.train.ExponentialMovingAverage(decay=0.5)  
       def mean_var_with_update():  
           ema_apply_op = ema.apply([batch_mean, batch_var])  
           with tf.control_dependencies([ema_apply_op]):  
                return tf.identity(batch_mean),tf.identity(batch_var)  
       # train_phase 訓練還是測試的flag  
       # 訓練階段計算runing_mean和runing_var，使用mean_var_with_update（）函數  
       # 測試的時候直接把之前計算的拿去用 ema.average(batch_mean)  
       mean, var = tf.cond(train_phase, mean_var_with_update,  
                            lambda:(ema.average(batch_mean), ema.average(batch_var)))  
       normed = tf.nn.batch_normalization(x, mean, var, beta, gamma, 1e-3)  
   return normed

至於此行代碼tf.nn.batch_normalization()就是簡單的計算batchnorm過程，這個函數所實現的功能就如此公式：

def batch_normalization(x, mean, variance, offset,scale, variance_epsilon, name=None):  
   with ops.name_scope(name, "batchnorm", [x, mean, variance,scale, offset]):  
       inv = math_ops.rsqrt(variance + variance_epsilon)  
    if scale is not None:  
           inv *= scale        
       return x * inv + (offset - mean * inv  
                       if offset is not Noneelse -mean * inv)

##Batch Normalization的帶來的優勢：

沒有它之前，需要小心的調整學習率和權重初始化，但是有了BN可以放心的使用大學習率，但是使用了BN，就不用小心的調參了，較大的學習率極大的提高了學習速度，

Batchnorm本身上也是一種正則的方式，可以代替其他正則方式如dropout等

另外，個人認為，batchnorm降低了數據之間的絕對差異，有一個去相關的性質，更多的考慮相對差異性，因此在分類任務上具有更好的效果

#Group Normalization
group normalization是2018年3月份何愷明大神的又一力作，優化了batch normalization在比較小的batch size 情況下表現不太好的劣勢。批量維度進行歸一化會帶來一些問題——批量統計估算不準確導致批量變小時，BN 的誤差會迅速增加。在訓練大型網絡和將特徵轉移到計算機視覺任務中（包括檢測、分割和視頻），內存消耗限制了只能使用小批量的BN。尤其是在我的破電腦裡面，batch的大小一般都是使用的1，相當於不存在BN。

下圖是論文中給出BN和GN的對比：

可以看出在bath size比較小的情況下，BN的性能十分地差，而GN的性能基本上沒有太大改變。

##Group Normalization 原理：
先給出他目前出現比較多的幾種normalization的示意圖：

BatchNorm：batch方向做歸一化，算NHW的均值

LayerNorm：channel方向做歸一化，算CHW的均值

InstanceNorm：一個channel內做歸一化，算H*W的均值

GroupNorm：將channel方向分group，然後每個group內做歸一化，算(C//G)HW的均值

從示意圖中看，也可以看出其實沒有太大的變化，所以代碼中也沒有需要太大的變動，只需要稍微修改一下就好了。

GN程式碼範例：

def GroupNorm(x,G=16,eps=1e-5):    
    N,H,W,C=x.shape         
    x=tf.reshape(x,[tf.cast(N,tf.int32),tf.cast(H,tf.int32),tf.cast(W,tf.int32),tf.cast(G,tf.int32),tf.cast(C//G,tf.int32)])    
    mean,var=tf.nn.moments(x,[1,2,4],keep_dims=True)    
    x=(x-mean)/tf.sqrt(var+eps)    
    x=tf.reshape(x,[tf.cast(N,tf.int32),tf.cast(H,tf.int32),tf.cast(W,tf.int32),tf.cast(C,tf.int32)])    
    gamma = tf.Variable(tf.ones(shape=[1,1,1,tf.cast(C,tf.int32)]), name="gamma")    
    beta = tf.Variable(tf.zeros(shape=[1,1,1,tf.cast(C,tf.int32)]), name="beta")    
    return x*gamma+beta

Group Normalization in Keras

其實也是在keras中的BatchNormalization層上進行一定的修改就得到了GroupNormalization層。正常和batchnormalization一樣的調用即可。但注意需要保持channel數是group的整數倍。

from keras.engine import Layer, InputSpec
from keras import initializers
from keras import regularizers
from keras import constraints
from keras import backend as K

from keras.utils.generic_utils import get_custom_objects


class GroupNormalization(Layer):
    """Group normalization layer

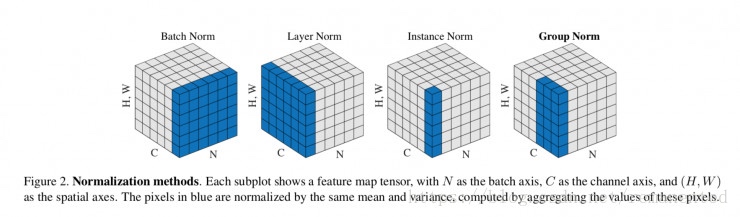
    Group Normalization divides the channels into groups and computes within each group
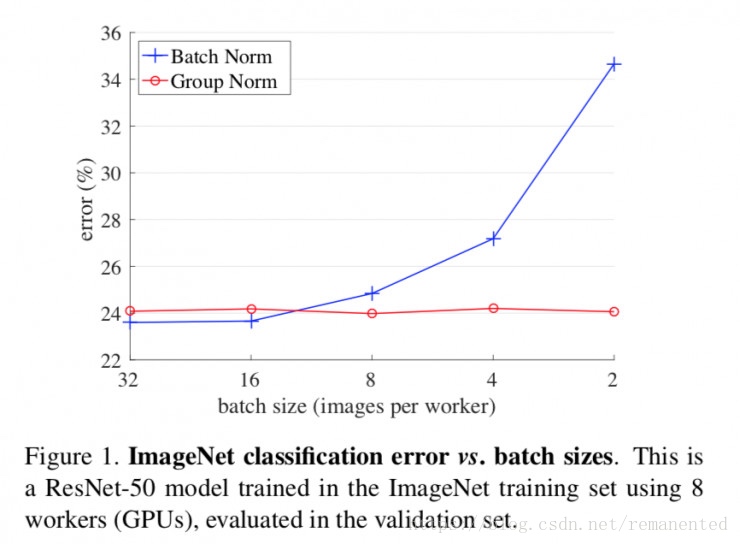
    the mean and variance for normalization. GN's computation is independent of batch sizes,
    and its accuracy is stable in a wide range of batch sizes

    # Arguments
        groups: Integer, the number of groups for Group Normalization.
        axis: Integer, the axis that should be normalized
            (typically the features axis).
            For instance, after a `Conv2D` layer with
            `data_format="channels_first"`,
            set `axis=1` in `BatchNormalization`.
        epsilon: Small float added to variance to avoid dividing by zero.
        center: If True, add offset of `beta` to normalized tensor.
            If False, `beta` is ignored.
        scale: If True, multiply by `gamma`.
            If False, `gamma` is not used.
            When the next layer is linear (also e.g. `nn.relu`),
            this can be disabled since the scaling
            will be done by the next layer.
        beta_initializer: Initializer for the beta weight.
        gamma_initializer: Initializer for the gamma weight.
        beta_regularizer: Optional regularizer for the beta weight.
        gamma_regularizer: Optional regularizer for the gamma weight.
        beta_constraint: Optional constraint for the beta weight.
        gamma_constraint: Optional constraint for the gamma weight.

    # Input shape
        Arbitrary. Use the keyword argument `input_shape`
        (tuple of integers, does not include the samples axis)
        when using this layer as the first layer in a model.

    # Output shape
        Same shape as input.

    # References
        - [Group Normalization](https://arxiv.org/abs/1803.08494)
    """

    def __init__(self,
                 groups=32,
                 axis=-1,
                 epsilon=1e-5,
                 center=True,
                 scale=True,
                 beta_initializer='zeros',
                 gamma_initializer='ones',
                 beta_regularizer=None,
                 gamma_regularizer=None,
                 beta_constraint=None,
                 gamma_constraint=None,
                 **kwargs):
        super(GroupNormalization, self).__init__(**kwargs)
        self.supports_masking = True
        self.groups = groups
        self.axis = axis
        self.epsilon = epsilon
        self.center = center
        self.scale = scale
        self.beta_initializer = initializers.get(beta_initializer)
        self.gamma_initializer = initializers.get(gamma_initializer)
        self.beta_regularizer = regularizers.get(beta_regularizer)
        self.gamma_regularizer = regularizers.get(gamma_regularizer)
        self.beta_constraint = constraints.get(beta_constraint)
        self.gamma_constraint = constraints.get(gamma_constraint)

    def build(self, input_shape):
        dim = input_shape[self.axis]

        if dim is None:
            raise ValueError('Axis ' + str(self.axis) + ' of '
                                                        'input tensor should have a defined dimension '
                                                        'but the layer received an input with shape ' +
                             str(input_shape) + '.')

        if dim < self.groups:
            raise ValueError('Number of groups (' + str(self.groups) + ') cannot be '
                                                                       'more than the number of channels (' +
                             str(dim) + ').')

        if dim % self.groups != 0:
            raise ValueError('Number of groups (' + str(self.groups) + ') must be a '
                                                                       'multiple of the number of channels (' +
                             str(dim) + ').')

        self.input_spec = InputSpec(ndim=len(input_shape),
                                    axes={self.axis: dim})
        shape = (dim,)

        if self.scale:
            self.gamma = self.add_weight(shape=shape,
                                         name='gamma',
                                         initializer=self.gamma_initializer,
                                         regularizer=self.gamma_regularizer,
                                         constraint=self.gamma_constraint)
        else:
            self.gamma = None
        if self.center:
            self.beta = self.add_weight(shape=shape,
                                        name='beta',
                                        initializer=self.beta_initializer,
                                        regularizer=self.beta_regularizer,
                                        constraint=self.beta_constraint)
        else:
            self.beta = None
        self.built = True

    def call(self, inputs, **kwargs):
        input_shape = K.int_shape(inputs)
        # Prepare broadcasting shape.
        ndim = len(input_shape)
        reduction_axes = list(range(len(input_shape)))
        del reduction_axes[self.axis]
        broadcast_shape = [1] * len(input_shape)
        broadcast_shape[self.axis] = input_shape[self.axis]

        reshape_group_shape = list(input_shape)
        reshape_group_shape[self.axis] = input_shape[self.axis] // self.groups
        group_shape = [-1, self.groups]
        group_shape.extend(reshape_group_shape[1:])
        group_reduction_axes = list(range(len(group_shape)))

        # Determines whether broadcasting is needed.
        needs_broadcasting = (sorted(reduction_axes) != list(range(ndim))[:-1])

        inputs = K.reshape(inputs, group_shape)

        mean = K.mean(inputs, axis=group_reduction_axes[2:], keepdims=True)
        variance = K.var(inputs, axis=group_reduction_axes[2:], keepdims=True)

        inputs = (inputs - mean) / (K.sqrt(variance + self.epsilon))

        original_shape = [-1] + list(input_shape[1:])
        inputs = K.reshape(inputs, original_shape)

        if needs_broadcasting:
            outputs = inputs

            # In this case we must explicitly broadcast all parameters.
            if self.scale:
                broadcast_gamma = K.reshape(self.gamma, broadcast_shape)
                outputs = outputs * broadcast_gamma

            if self.center:
                broadcast_beta = K.reshape(self.beta, broadcast_shape)
                outputs = outputs + broadcast_beta
        else:
            outputs = inputs

            if self.scale:
                outputs = outputs * self.gamma

            if self.center:
                outputs = outputs + self.beta

        return outputs

    def get_config(self):
        config = {
            'groups': self.groups,
            'axis': self.axis,
            'epsilon': self.epsilon,
            'center': self.center,
            'scale': self.scale,
            'beta_initializer': initializers.serialize(self.beta_initializer),
            'gamma_initializer': initializers.serialize(self.gamma_initializer),
            'beta_regularizer': regularizers.serialize(self.beta_regularizer),
            'gamma_regularizer': regularizers.serialize(self.gamma_regularizer),
            'beta_constraint': constraints.serialize(self.beta_constraint),
            'gamma_constraint': constraints.serialize(self.gamma_constraint)
        }
        base_config = super(GroupNormalization, self).get_config()
        return dict(list(base_config.items()) + list(config.items()))

    def compute_output_shape(self, input_shape):
        return input_shape